原文链接：http://t.csdnimg.cn/DY7gy

环形缓冲区是嵌入式系统中十分重要的一种数据结构，比如在串口处理中，串口中断接收数据直接往环形缓冲区丢数据，而应用可以从环形缓冲区取数据进行处理，这样数据在读取和写入的时候都可以在这个缓冲区里循环进行，程序员可以根据自己需要的数据大小来决定自己使用的缓冲区大小，不用担心数组越界。

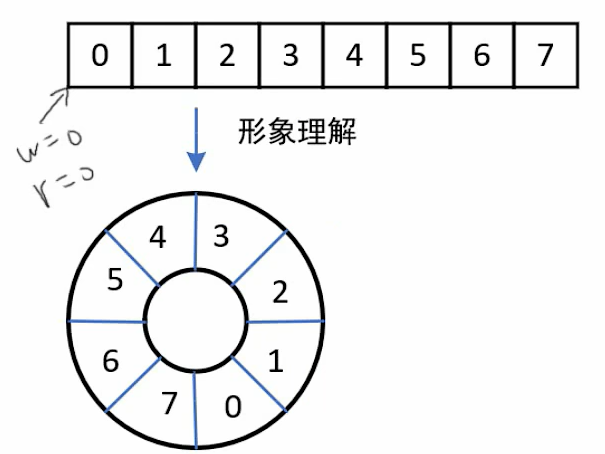
image-20240203112201743

队列的基本概念：队列 (Queue)：是一种先进先出(First In First Out ,简称 FIFO)的线性表，只允许在一端插入（入队），在另一端进行删除（出队）。

队列头就是指向已经存储的数据，并且这个数据是待处理的。下一个CPU处理的数据就是1；而队列尾则指向可以进行写数据的地址。

队列是什么

队列是一种很常见的数据结构，满足先进先出的方式，如果我们设定队列的最大长度，那就意味着进队列和出队列的元素的数量实则满足一种动态平衡。

如果我们把首次添加入队列的元素作为一个一维坐标的原点，那么随着队列中元素的添加，坐标原点到队尾元素的长度会无穷无尽的增大，随这之前添入的元素不断出列，对头对应的下标点也在不断增大。这样，进队列和出队列的元素的数量就对应到对头和队尾下标点的移动

因此我们评判一个队列长度是否溢出原先约定的最大长度，实则就是在评判队尾坐标点与队头坐标点之间的差值，无论是出队列还是入队列，队头和队尾的坐标都在不断增大

img

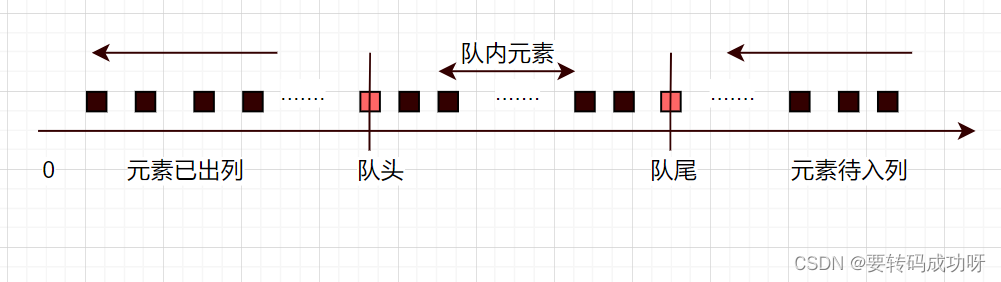
front指针和rear指针的引入

虽然队尾和队头的下标在不断增大，但是我们对于队列的研究只需要局限在队头与队尾之间的元素，坐标原点到队头之间的元素已经算作出列元素，并不需要研究。因此我们不妨将队列在逻辑上放入一个事先设定容量的一维数组中，只要这个数组的容量是队列中元素的个数+1就行，为什么要这么设定待会再讲。我们想要达到的目的是，无论出列还是入列，本质上是通过修改数组中元素的值，那些已经出列的元素所在的下标位需要放置新入列的元素，并在逻辑上保证新入列元素位于队尾就行。

因此，我们不得不得引入头指针front和尾指针rear，对指针指向的数组下标对应空间进行操作，来修改数组中元素的值。

front指针和rear指针的理解

front：初始值为0，对应索引位待出列，若当前指向的数组下标的元素要出列，则先执行出列动作(实际上不用操作，出列的索引位可以被新入队的元素覆盖)，随后front指针就要向后一位，即front++

rear：初始值为0，对应索引位待入列，若当前指向的数组下标有元素要入列，则先执行入列动作（索引位元素赋值），随后front指针就要向后一位，即rear++

队列最大长度匹配数组容量导致一种错误的解决方案

这就会有一个问题，随着队列中元素的不断更迭，front和rear很快就会超过数组容量，造成数组索引越界

img

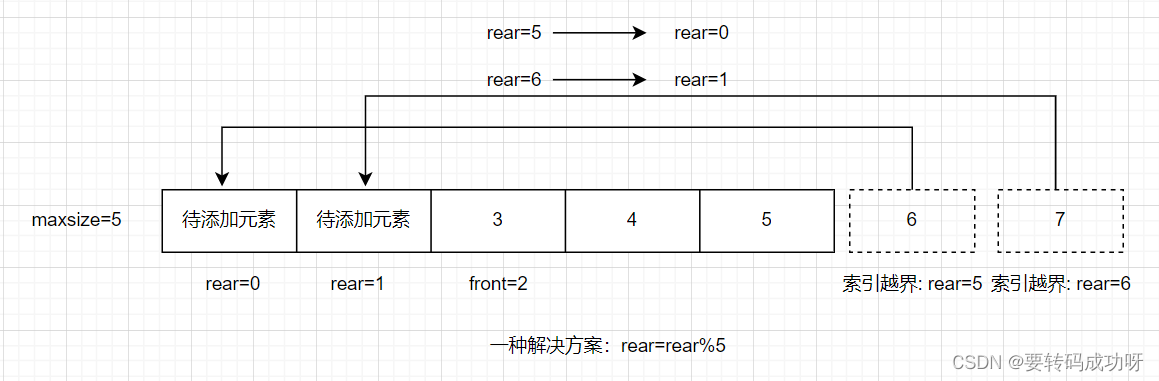
比如上图所示，front=2，也就是说已经有两个元素出列了，因此rear=5与rear=6对应的两个元素理应可以入列，但是我们发现数组maxsize=5，不存在索引位5和6，强行对这两个下标赋值会造成索引越界异常indexOutException 。但是我们发现此时数组中索引位0和1都空着，完全可以将这两个位置利用起来，因此我们可以想办法让实际的rear值转化为等效的rear值，也就是是让rear=5转化为rear=0，同理rear6转化为rear=1。怎么做到呢？无疑是通过取余！

每次新元素入队后， 执行rear=(rear)%maxSize操作，随后执行rear++操作右移rear指针

像上图中的rear=rear%5乍一看好像没问题，但实际上这种取余方式是有问题的，出现这种取余方式的根源在于我们想让队列最大长度与数组容量保持一致，下文会详细说明这种解决方案的错误之处。

指针的往复移动：逻辑上的环形

出队和入队的方向是从右向左，而front与rear指针的移动方向却是从左到右循环往复（指向数组末尾后按照取余算法又重置为数组开头），因此我们可以把单向数组在逻辑上理解成环形数组，指针的循环往复移动理解成按照顺时针或逆时针（只要规定某一方向就好）单向移动

环形队列小知识：

环形队列是在实际编程极为有用的数据结构,它有如下特点。

它是一个首尾相连的FIFO的数据结构，采用数组的线性空间,数据组织简单。能很快知道队列是否满为空。能以很快速度的来存取数据。

因为有简单高效的原因，甚至在硬件都实现了环形队列。

环形队列广泛用于网络数据收发，和不同程序间数据交换（比如内核与应用程序大量交换数据,从硬件接收大量数据）均使用了环形队列。

队列为空的判别

我们怎么判断队列为空呢？

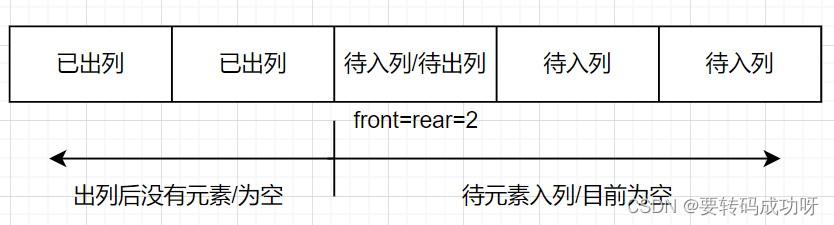
如果我们按照指针从左到右的方向移动，当front指针和rear指针重合时，front指针对应的索引位之前的索引位都已经出列完毕，而rear指针对应的索引位以及之后的所有索引位还未有元素入列。

所以队列是否为空的判别：front==rear

img

rear=rear%maxSize解决方案的问题

入队图示
下图展示了maxSize=5的数组中，front=0保持不变，元素依次入列直到满载，rear指针的移动情况：

img

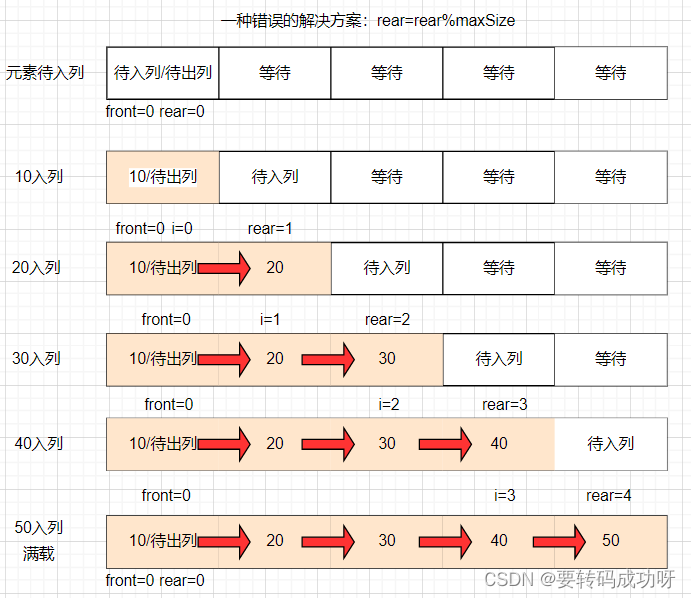
front=rear=0的歧义
可以看到，如果我们认为队列容量与数组容量应该持平，那么当第五个元素50入列后，本来rear=4执行了rear++的操作后，rear=5，随后rear将会通过取余算法rear=rear%maxSize重置为0，这是我们解决方案的核心！

但关键点就在这里，我们发现空载时front=rear=0，满载时依然有front=rear=0！这样子我们就无法判断front=rear时，队列是空还是满，因此rear=rear%maxSize这种解决方案是不被允许的

新的解决方案：置空位的引入

新的解决方案
每次新元素入队后， 执行rear=(rear+1)%maxSize操作，该操作包含rear++操作

置空位的引入
并且我们人为规定，数组中必须留有一个索引位不得放置元素，必须置空！！！如何实现我们的人为规定呢？那就要先探索当数组满载后front和rear指针之间有啥关系

入队图示
下图展示了maxSize=5的数组中，front=0保持不变，元素依次入列直到满载，rear指针的移动情况：

img

   人为的让最后一位置空，所以当元素40入列后，数组已经满载

   满载后数据之间的关系：

front=0
rear=(rear+1)%maxSize=(3+1)%5=4 (注： 执行完arr[rear]=40，再执行 rear=(rear+1)%maxSize)
(rear+1)%maxSize=(4+1)%5=0=front
当我们认为的满载发生后，最后一位置空，发现此时rear和front之间的关系为(rear+1)%maxSize=(4+1)%5=0=front，因此这个关系可以作为满载的条件

   因为处于满载状态，我们无法再往队列添加元素，只能从队列取出元素，也就是进行出列的操作，而一旦我们执行了出列的操作，比如将索引位i=0上的元素10出列后，则front右移，即执行front=(front+1)%maxSize操作，最终front=1。

   若随后又添加元素入列，即在索引位i=4上添加元素50，随后又会执行rear=(rear+1)%maxSize操作，最终rear=0。

   rear=0≠front=1，此时就不会出现之前那种错误方案中 rear=front=0导致歧义的情况，而一旦 rear=front=0，必然表示队列为空，因此这种解决方案是行得通的

队列为满的判别

​ 当我们认为的满载发生后，最后一位置空，发现此时rear和front之间的关系为(rear+1)%maxSize=(4+1)%5=0=front，因此这个关系可以作为满载的条件

队列中元素的个数

​ numValid=(rear+maxSize-front)%maxSize，大家可以带入数据验证一下

 实际上：

   当rear在front之后(这里指的是数组中索引位的前后，并非逻辑上的前后)，有效数据个数=rear-front=(rear+maxSize-front)%maxSize

   当rear在front之前(这里指的是数组中索引位的前后，并非逻辑上的前后)，有效数据个数=(rear+maxSize-front)%maxSize

值得注意的一些细节

细节1
置空位虽然是人为引入的，但这不意味这置空位的位置是随意的，实际上，只有队列满后才会将剩下的位置作为置空位，一旦置空位出现，rear和front永远不可能指向同一个索引位，因为你会惊奇的发现置空位恰号将rear和front隔开了.

 置空位就像一把锁，一旦上锁就只能通过出队列操作解锁

继续执行获取元素操作出队列（解锁）：

img

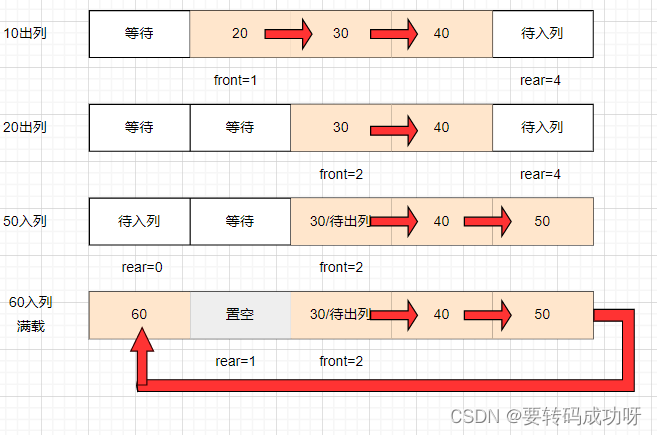
上图中60入列后满载，可以看到置空位再次出现，但30➡40➡50➡60➡置空位 形成了逻辑上的闭环

细节2
从闭环的角度理解，front永远不可能在循环中超过rear，最多只能和rear相遇。

因为置空位的出现，rear不可能拉front一圈，也就避免了rear在超过front的情况下主动与front相遇

下图中的maxSize-1对应的就是置空位，rear是无法越过置空位的。只有front主动顺时针追赶上rear，它俩才会相遇，而此时队列内就没有元素，为空

img

细节3
队列的最大长度queueMaxsize=数组容量arrayMaxSize-1 （由于置空位要占一位）

实例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#define RINGBUFF_LEN 256;
//定义一个缓冲区结构体
typedef struct
{
    u16 Head;           
    u16 Tail;
    u8 Ring_Buff[RINGBUFF_LEN];
}RingBuff_t;

/*若想更灵活，可以用动态内存分配方式（如使用指针）来实现可变长度的缓冲区
typedef struct
{
u16 Head;
u16 Tail;
u8* Ring_Buff;
}RingBuff_t;

// 初始化函数，传入所需长度
void RingBuff_Init(RingBuff_t rbuff, size_t len)
{
    rbuff->Head = 0;
    rbuff->Tail = 0;
    rbuff->Ring_Buff = (u8)malloc(len * sizeof(u8));
    if (!rbuff->Ring_Buff) {
    // 处理内存分配失败的情况...
    }
}
在C语言中，u8* Ring_Buff; 是一个指向无符号8位整型（通常代表字节）的指针。它本身并不是一个数组，但可以用来指向一块内存区域，这块内存可以被当作数组来处理。

当你通过 malloc 函数为 Ring_Buff 分配了足够长度的内存后，你就可以像操作数组那样对这块内存进行读写
*/

//创建一个ringBuff的缓冲区
RingBuff_t ringBuff;

//初始化环形缓冲区
void RingBuff_Init(void)
{
   //初始化相关信息
   ringBuff.Head = 0;
   ringBuff.Tail = 0;
}

//写数据
u8 Write_RingBuff(u8 data)
{
    if(ringBuff.Head=(ringBuff.Tail+1)%maxSize) //缓冲区满
    {
      return FLASE;
    }

    ringBuff.Ring_Buff[ringBuff.Tail]=data;//在Tail对应索引位写入数据
    ringBuff.Tail=(ringBuff.Tail+1)%RINGBUFF_LEN; //ringBuff.Tail++; 防止越界非法访问
    return TRUE;
}

//读数据
10u8 Read_RingBuff(u8 *rData)
11{
12   if(ringBuff.Head==ringBuff.Tail)//判断非空
13    {
14       return FLASE;
15    }
    
16   *rData = ringBuff.Ring_Buff[ringBuff.Head];//先进先出FIFO，从缓冲区头出

18   ringBuff.Head = (ringBuff.Head+1)%RINGBUFF_LEN;// ringBuff.Head++;防止越界非法访问
    
20   return TRUE;
21}